Aluminum Roof Rib-Joist Calculations

Aluminum Roof Rib-Joist Calculations with Python

Calculating and Visualizing Arc Lengths for Aluminum Roofs and Plywood Rib Joists with Python, Quarto and Visual Studio Code as starting point for CNC iterations.

TL;DR

This guide covers the arc length calculations for a aluminum roofs that will have undermounted curving plywood rib joists. These calculations are intended for initial cutting with CNC, but lengths and dimensions may need to be adjusted as we refine the process. Below, we compute and visualize the arc radii, heights, and key dimensions. While this version provides the base design, we expect iterative modifications as we cut, test, and adjust dimensions before finalizing in “Part 2.”

---

Requirements Recap

Three Arcs to Calculate:

1. Aluminum Roof (Arc 1) – The main arc defining the roof’s curve.
2. Top of Plywood Arch (Arc 2) – Offset by a 2-inch air gap below the roof.
3. Bottom of Plywood Arch (Arc 3) – Offset by the 10-inch plywood rib height from the top arch.

Additional Project Details:

• Building Width: Total width = 375 inches (31’ 2.375”).
• Air Gap: We’re starting with a 2-inch air gap, but we can adjust this if needed after the first cuts.
• Plywood Rib Height: 10 inches tall per rib, but this height may also vary depending on fit and results from initial testing.

---

Objectives

Primary Goals:

1. Calculate the radius and arc lengths for all three arcs.
2. Plot and visualize these arcs to preview the cuts.
3. Label key dimensions and angles directly on the plot.
4. Segment the area between the arcs for efficient plywood usage (4x8 sheets).
5. Generate partial rib segments for CNC cutting, while remaining open to modifying these segments in later iterations.

Notes on Extensibility

This guide is designed as a starting point & proof of concept for a custom build still in design. No plan survives first contact with the material: the dimensions, angles, and cutting process may evolve after the first rounds on the CNC. Once we cut the initial iterations, we’ll fine-tune based on what we observe, and come back to write “Part 2” with the finalized parameters.

---

Mathematical Formulas

Radius of Curvature

The radius \[ R \] for each arc is calculated using the following formula, derived from circular arc geometry: \[R = \frac{4H^2 + L^2}{8H}\] Where: \(H\) = height of the arc & \(L\) = chord length (the building’s width).

Arc Length

The arc length (\(L_{arc}\)) of each arc is given by the formula for a semicircle: \[L_{arc} = \pi \times R\] Where \(R\) is the radius calculated above.

---

Python Setup 🐍

# Initing vars ⏳...
import numpy as np
import matplotlib.pyplot as plt
from IPython.display import display, Markdown

# Constants
INCHES_PER_FOOT = 12
PLYWOOD_WIDTH = 96   # inches (8 feet)
PLYWOOD_LENGTH = 96  # inches (8 feet)

# Default Project Dimensions
DEFAULT_WIDTH_FEET = 31
DEFAULT_WIDTH_INCHES = 3
DEFAULT_HEIGHT_FEET = 11
DEFAULT_HEIGHT_INCHES = 2.375
DEFAULT_AIR_GAP_INCHES = 2  # inches (air gap between aluminum and top of plywood arch)
DEFAULT_RIB_HEIGHT_INCHES = 10  # inches (height of the plywood rib)

---

Function Definitions

1. Functions for Radius and Arc Length Calculation 🐍

# Convert feet and inches to total inches for easy dimensional calculations
def convert_to_inches(feet, inches):
    return feet * INCHES_PER_FOOT + inches

# Calculates the radius of curvature based on the height and width of the arc
def calculate_radius(H, L):
    """
    Calculate the radius of an arc using the formula:
    R = (4H^2 + L^2) / (8H)
    """
    return (4 * H**2 + L**2) / (8 * H)

# Calculate arc lengths for the aluminum roof and the plywood rib
def calculate_arc_lengths(width, height_roof, air_gap, rib_height):
    """
    Calculate radii and arc lengths for the aluminum roof (top), 
    top of the plywood rib, and bottom of the plywood rib.
    """
    # Calculate radius and arc length for the aluminum roof (Arc 1)
    radius_roof = calculate_radius(height_roof, width)
    arc_length_roof = np.pi * radius_roof

    # Calculate radius and arc length for the top of the plywood rib (Arc 2)
    height_rib_top = height_roof + air_gap
    radius_rib_top = calculate_radius(height_rib_top, width)
    arc_length_rib_top = np.pi * radius_rib_top

    # Calculate radius for the bottom of the plywood rib (Arc 3)
    radius_rib_bottom = radius_rib_top - rib_height
    arc_length_rib_bottom = np.pi * radius_rib_bottom

    return {
        "radius_roof": radius_roof,
        "arc_length_roof": arc_length_roof,
        "radius_rib_top": radius_rib_top,
        "arc_length_rib_top": arc_length_rib_top,
        "radius_rib_bottom": radius_rib_bottom,
        "arc_length_rib_bottom": arc_length_rib_bottom,
    }

---

2. Function for Plotting Arcs for Visualization 🐍

# Generate theta values for plotting the arcs (from 0 to pi)
def plot_arcs(width, height_roof, air_gap, rib_height):
    """
    Plot the aluminum roof arc, top of plywood rib arc, and bottom of plywood rib arc.
    Annotate relevant dimensions and angles.
    """
    arc_data = calculate_arc_lengths(width, height_roof, air_gap, rib_height)

    # Generating theta values for the arcs
    num_points = 100
    theta = np.linspace(0, np.pi, num_points)

    # Generate x and y coordinates for each arc, shifted to start from (0,0)
    x_roof = arc_data['radius_roof'] * np.cos(theta) + (width / 2) + INCHES_PER_FOOT
    y_roof = arc_data['radius_roof'] * np.sin(theta)

    x_rib_top = arc_data['radius_rib_top'] * np.cos(theta) + (width / 2) + INCHES_PER_FOOT
    y_rib_top = arc_data['radius_rib_top'] * np.sin(theta)

    x_rib_bottom = arc_data['radius_rib_bottom'] * np.cos(theta) + (width / 2) + INCHES_PER_FOOT
    y_rib_bottom = arc_data['radius_rib_bottom'] * np.sin(theta)

    # Plotting the arcs
    plt.figure(figsize=(12, 8.5))

    plt.plot(x_roof, y_roof, label='Aluminum Roof (Arc 1)', color='grey')
    plt.plot(x_rib_top, y_rib_top, label='Top of Plywood Rib (Arc 2)', color='black', linestyle='--')
    plt.plot(x_rib_bottom, y_rib_bottom, label='Bottom of Plywood Rib (Arc 3)', color='brown', linestyle='-.')

    # Annotate arc lengths
    plt.text(width / 2, arc_data['radius_rib_bottom'] - 8, f"Arc 1 Length: {arc_data['arc_length_roof']:.2f} in", color='grey')
    plt.text(width / 2, arc_data['radius_rib_bottom'] - 12, f"Arc 2 Length: {arc_data['arc_length_rib_top']:.2f} in", color='black')
    plt.text(width / 2, arc_data['radius_rib_bottom'] - 16, f"Arc 3 Length: {arc_data['arc_length_rib_bottom']:.2f} in", color='brown')

    # Visualizing air gap and rib height
    plt.vlines(x=width / 2, ymin=y_rib_top[0], ymax=y_roof[0], color='purple', linestyle='-', linewidth=2, label=f'Air Gap: {air_gap} in')
    plt.vlines(x=width / 2, ymin=y_rib_bottom[0], ymax=y_rib_top[0], color='orange', linestyle='-', linewidth=2, label=f'Plywood Rib Height: {rib_height} in')

    plt.xticks(np.arange(0, width + 24, 12))
    plt.yticks(np.arange(0, arc_data['radius_rib_bottom'] + 24, 12))
    plt.grid(True)

    # Plot settings
    plt.xlabel('Width (inches)')
    plt.ylabel('Height (inches)')
    plt.title('Visualization of Aluminum Roof and Plywood Rib Arcs (Upper Right Quadrant)')
    plt.axhline(0, color='black', lw=0.5)
    plt.axvline(0, color='black', lw=0.5)
    plt.legend()
    plt.tight_layout()
    plt.show()
    print("Plotting complete... ✅")

3. Function to Create Installer Facing Markdown Output 🐍

# Displaying the Markdown output for installers
def extended_data_dump(width, height_roof, air_gap, rib_height):
    """
    Provides a full extended data dump with radii, arc lengths, and angles for Arc 1 (Aluminum Roof),
    Arc 2 (Top of Plywood Rib), and Arc 3 (Bottom of Plywood Rib).
    This data is useful for fabricators and installers.
    """
    # Calculate arc data
    arc_data = calculate_arc_lengths(width, height_roof, air_gap, rib_height)

    # Calculate key values for the dump
    arc_lengths = {
        "arc_1": arc_data['arc_length_roof'],
        "arc_2": arc_data['arc_length_rib_top'],
        "arc_3": arc_data['arc_length_rib_bottom']
    }

    radii = {
        "radius_roof": arc_data['radius_roof'],
        "radius_rib_top": arc_data['radius_rib_top'],
        "radius_rib_bottom": arc_data['radius_rib_bottom']
    }

    # Print the extended data dump
    print("\n## Raw Markdown Data for Fabricators & Installers\n")
    
    print(f"Width of Building: {width:.2f} inches")
    print(f"Height of Aluminum Roof: {height_roof:.2f} inches")
    print(f"Air Gap: {air_gap:.2f} inches")
    print(f"Plywood Rib Height: {rib_height:.2f} inches")
    
    print("\n### Arc Lengths\n")
    print(f"- **Arc 1 (Aluminum Roof)** Length: {arc_lengths['arc_1']:.2f} inches")
    print(f"- **Arc 2 (Top of Plywood Rib)** Length: {arc_lengths['arc_2']:.2f} inches")
    print(f"- **Arc 3 (Bottom of Plywood Rib)** Length: {arc_lengths['arc_3']:.2f} inches")
    
    print("\n### Radii\n")
    print(f"- **Radius of Arc 1 (Aluminum Roof)**: {radii['radius_roof']:.2f} inches")
    print(f"- **Radius of Arc 2 (Top of Plywood Rib)**: {radii['radius_rib_top']:.2f} inches")
    print(f"- **Radius of Arc 3 (Bottom of Plywood Rib)**: {radii['radius_rib_bottom']:.2f} inches")

    # Now compute the corresponding angles for Arc 1, Arc 2, and Arc 3
    angle_arc_1 = np.pi  # since it's a semicircle, angle is always pi radians (180 degrees)
    angle_arc_2 = np.pi
    angle_arc_3 = np.pi
    
    print("\n### Angles\n")
    print(f"- **Angle for Arc 1 (Aluminum Roof)**: {np.degrees(angle_arc_1):.2f} degrees")
    print(f"- **Angle for Arc 2 (Top of Plywood Rib)**: {np.degrees(angle_arc_2):.2f} degrees")
    print(f"- **Angle for Arc 3 (Bottom of Plywood Rib)**: {np.degrees(angle_arc_3):.2f} degrees")

    print("\n### Notes for Fabricators and Installers\n")
    print("The above data shows the radii and arc lengths for each of the three arcs.")
    print("These dimensions are essential for cutting and assembling the plywood ribs.")
    print("The angles for each arc are constant at 180 degrees, assuming a perfect semicircular shape.")
    print("Ensure that the calculated air gap and rib height are maintained throughout the installation.")

---

Result & Plot 🐍

# Plotting full curves & dumping data⏳...
width_in_inches = convert_to_inches(DEFAULT_WIDTH_FEET, DEFAULT_WIDTH_INCHES)
height_roof = convert_to_inches(DEFAULT_HEIGHT_FEET, DEFAULT_HEIGHT_INCHES)

plot_arcs(width_in_inches, height_roof, DEFAULT_AIR_GAP_INCHES, DEFAULT_RIB_HEIGHT_INCHES)

extended_data_dump(width_in_inches, height_roof, DEFAULT_AIR_GAP_INCHES, DEFAULT_RIB_HEIGHT_INCHES)

Plotting complete... ✅

## Raw Markdown Data for Fabricators & Installers

Width of Building: 375.00 inches
Height of Aluminum Roof: 134.38 inches
Air Gap: 2.00 inches
Plywood Rib Height: 10.00 inches

### Arc Lengths

- **Arc 1 (Aluminum Roof)** Length: 622.04 inches
- **Arc 2 (Top of Plywood Rib)** Length: 619.15 inches
- **Arc 3 (Bottom of Plywood Rib)** Length: 587.74 inches

### Radii

- **Radius of Arc 1 (Aluminum Roof)**: 198.00 inches
- **Radius of Arc 2 (Top of Plywood Rib)**: 197.08 inches
- **Radius of Arc 3 (Bottom of Plywood Rib)**: 187.08 inches

### Angles

- **Angle for Arc 1 (Aluminum Roof)**: 180.00 degrees
- **Angle for Arc 2 (Top of Plywood Rib)**: 180.00 degrees
- **Angle for Arc 3 (Bottom of Plywood Rib)**: 180.00 degrees

### Notes for Fabricators and Installers

The above data shows the radii and arc lengths for each of the three arcs.
These dimensions are essential for cutting and assembling the plywood ribs.
The angles for each arc are constant at 180 degrees, assuming a perfect semicircular shape.
Ensure that the calculated air gap and rib height are maintained throughout the installation.

---

Partial Rib Segments for CNC Cutting

Now, to continue plotting and representing how the partial rib segments can be cut from 4x8 plywood sheets.

Key Objectives

1. Complete Plotting of Partial Ribs: Finish representing how each rib segment is laid out across multiple plywood sheets.
2. Store and Verbosely Print Segment Information: Store each rib segment and print the dimensions for clarity.
3. Continue with Efficient Visualization: Provide a clear visual depiction of the partial rib segments.

---

4. Functions for Slicing & Plotting the Ribs for CNC Cutting 🐍:

# Normalize coordinates to fit within plywood dimensions
def normalize_coordinates(x_coords, y_coords, plywood_length, plywood_width):
    min_x = min(x_coords)
    min_y = min(y_coords)
    x_normalized = [x - min_x for x in x_coords]
    y_normalized = [y - min_y for y in y_coords]
    return x_normalized, y_normalized

# Function to slice and plot ribs and output all CNC data
def slice_and_output_ribs_for_cnc(width, height_roof, air_gap, rib_height, plywood_width=PLYWOOD_WIDTH, plywood_length=PLYWOOD_LENGTH):
    arc_data = calculate_arc_lengths(width, height_roof, air_gap, rib_height)
    total_arc_length = arc_data['arc_length_rib_top']
    num_segments = int(np.ceil(total_arc_length / plywood_length))
    segment_arc_length = total_arc_length / num_segments
    num_points = 1000
    theta_full = np.linspace(0, np.pi, num_points)
    arc_lengths_full = arc_data['radius_rib_top'] * theta_full
    theta_boundaries = [np.interp(i * segment_arc_length, arc_lengths_full, theta_full) for i in range(num_segments + 1)]

    # Output storage for all segment data
    full_output = []

    for i in range(num_segments):
        theta_start = theta_boundaries[i]
        theta_end = theta_boundaries[i + 1]
        theta_segment = np.linspace(theta_start, theta_end, num_points)
        x_top = arc_data['radius_rib_top'] * np.cos(theta_segment) + (width / 2)
        y_top = arc_data['radius_rib_top'] * np.sin(theta_segment)
        x_bottom = arc_data['radius_rib_bottom'] * np.cos(theta_segment) + (width / 2)
        y_bottom = arc_data['radius_rib_bottom'] * np.sin(theta_segment)

        # Offset and normalize coordinates for CNC plot
        x_offset = x_top[0]
        x_top_offset = x_top - x_offset
        x_bottom_offset = x_bottom - x_offset
        x_coords = list(x_top_offset) + list(x_bottom_offset)
        y_coords = list(y_top) + list(y_bottom)
        x_normalized, y_normalized = normalize_coordinates(x_coords, y_coords, plywood_length, plywood_width)
        x_top_normalized = x_normalized[:num_points]
        x_bottom_normalized = x_normalized[num_points:]
        y_top_normalized = y_normalized[:num_points]
        y_bottom_normalized = y_normalized[num_points:]

        # Store segment data
        segment_data = {
            "segment": i + 1,
            "theta_start": theta_start,
            "theta_end": theta_end,
            "top_left": (x_top_normalized[0], y_top_normalized[0]),
            "top_right": (x_top_normalized[-1], y_top_normalized[-1]),
            "bottom_left": (x_bottom_normalized[0], y_bottom_normalized[0]),
            "bottom_right": (x_bottom_normalized[-1], y_bottom_normalized[-1]),
            "arc_length_segment": segment_arc_length,
        }
        full_output.append(segment_data)

        # Output CNC cutting details
        print(f"### CNC Cutting Data for Segment {i + 1}")
        print(f"- Theta Start: {theta_start:.4f} rad, Theta End: {theta_end:.4f} rad")
        print(f"- **Top Left**: X: {segment_data['top_left'][0]:.2f}, Y: {segment_data['top_left'][1]:.2f}")
        print(f"- **Top Right**: X: {segment_data['top_right'][0]:.2f}, Y: {segment_data['top_right'][1]:.2f}")
        print(f"- **Bottom Left**: X: {segment_data['bottom_left'][0]:.2f}, Y: {segment_data['bottom_left'][1]:.2f}")
        print(f"- **Bottom Right**: X: {segment_data['bottom_right'][0]:.2f}, Y: {segment_data['bottom_right'][1]:.2f}")
        print(f"- **Arc Length for Segment**: {segment_arc_length:.2f} inches\n")
        
        # Plotting each segment for visualization
        plt.figure(figsize=(12, 8))
        plt.plot(x_top_normalized, y_top_normalized, label=f'Top Curve (Arc 2) of Segment {i + 1}', color='black')
        plt.plot(x_bottom_normalized, y_bottom_normalized, label=f'Bottom Curve (Arc 3) of Segment {i + 1}', color='brown', linestyle='--')
        plt.plot([x_top_normalized[0], x_bottom_normalized[0]], [y_top_normalized[0], y_bottom_normalized[0]], color='green', linestyle='--', label='Left Vertical Edge')
        plt.plot([x_top_normalized[-1], x_bottom_normalized[-1]], [y_top_normalized[-1], y_bottom_normalized[-1]], color='orange', linestyle='--', label='Right Vertical Edge')
        plt.xticks(np.arange(0, plywood_length + 1, 12))
        plt.yticks(np.arange(0, plywood_width + 1, 12))
        plt.grid(True)
        plt.xlabel('Length (inches)')
        plt.ylabel('Height (inches)')
        plt.title(f'Plywood Cutting Plan for Segment {i + 1}')
        plt.legend()

        # Label rib height for each segment
        plt.text(5, rib_height, f"Rib Height: {rib_height:.2f} in", rotation=0, va='center')
        plt.text(5, 5, f"Segment {i + 1}", fontsize=14, color='blue', bbox=dict(facecolor='white', alpha=0.5))
        plt.xlim(0, plywood_length)
        plt.ylim(0, plywood_width)
        plt.tight_layout()
        plt.show()

    # Print the Markdown data for fabricators and installers
    print("\n## Raw Markdown Data for Fabricators & Installers\n")
    for data in full_output:
        print(f"Segment {data['segment']}:")
        print(f"- Theta Start: {data['theta_start']:.4f} rad, Theta End: {data['theta_end']:.4f} rad")
        print(f"- Top Left: {data['top_left']}, Top Right: {data['top_right']}")
        print(f"- Bottom Left: {data['bottom_left']}, Bottom Right: {data['bottom_right']}")
        print(f"- Arc Length: {data['arc_length_segment']:.2f} inches\n")

---

Results & Plots 🐍

# Example usage of the function
width_in_inches = convert_to_inches(DEFAULT_WIDTH_FEET, DEFAULT_WIDTH_INCHES)
height_roof = convert_to_inches(DEFAULT_HEIGHT_FEET, DEFAULT_HEIGHT_INCHES)

# Call the function to slice and output with optimized plywood layout
slice_and_output_ribs_for_cnc(width_in_inches, height_roof, DEFAULT_AIR_GAP_INCHES, DEFAULT_RIB_HEIGHT_INCHES)

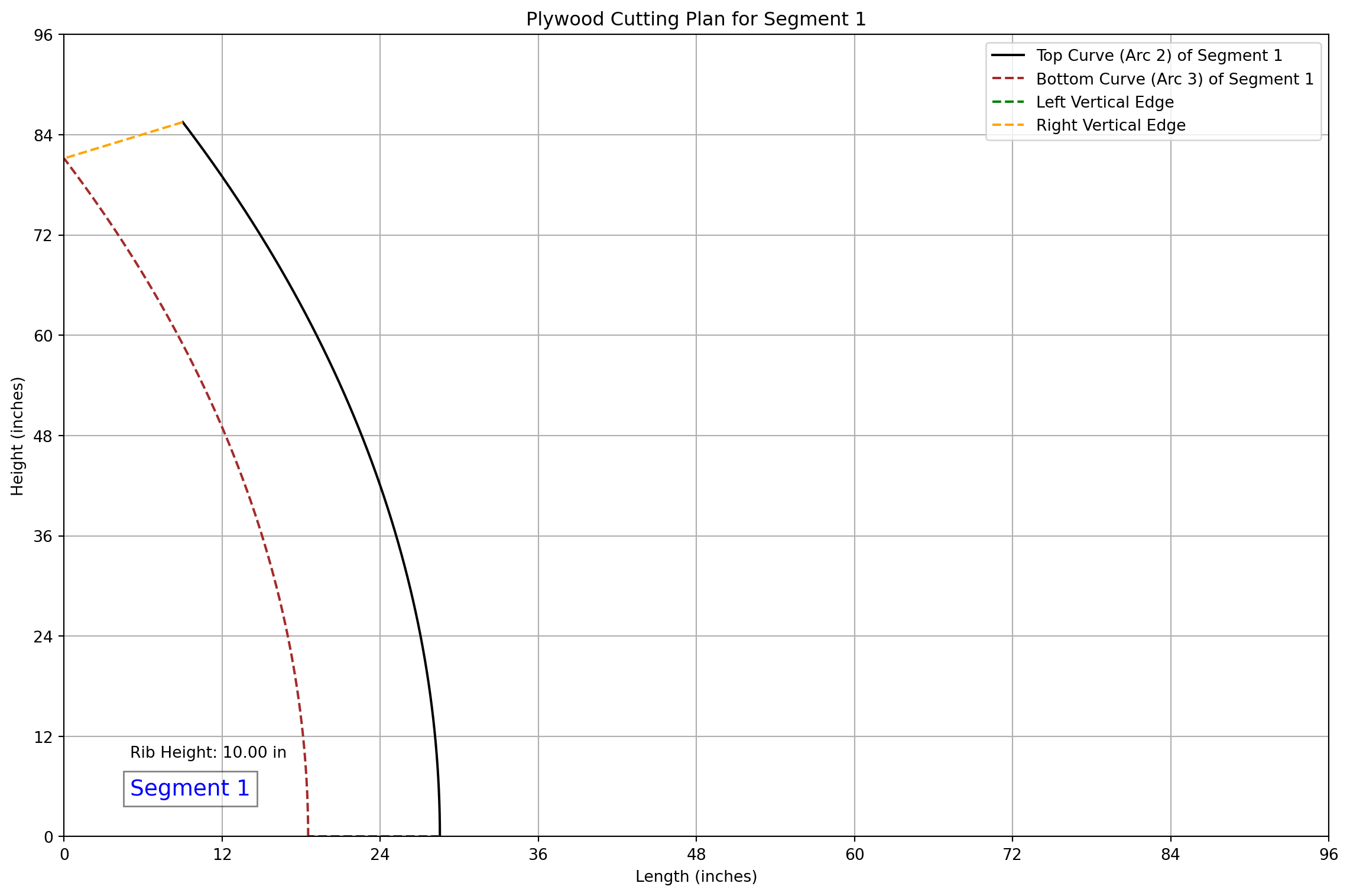
### CNC Cutting Data for Segment 1
- Theta Start: 0.0000 rad, Theta End: 0.4488 rad
- **Top Left**: X: 28.53, Y: 0.00
- **Top Right**: X: 9.01, Y: 85.51
- **Bottom Left**: X: 18.53, Y: 0.00
- **Bottom Right**: X: 0.00, Y: 81.17
- **Arc Length for Segment**: 88.45 inches

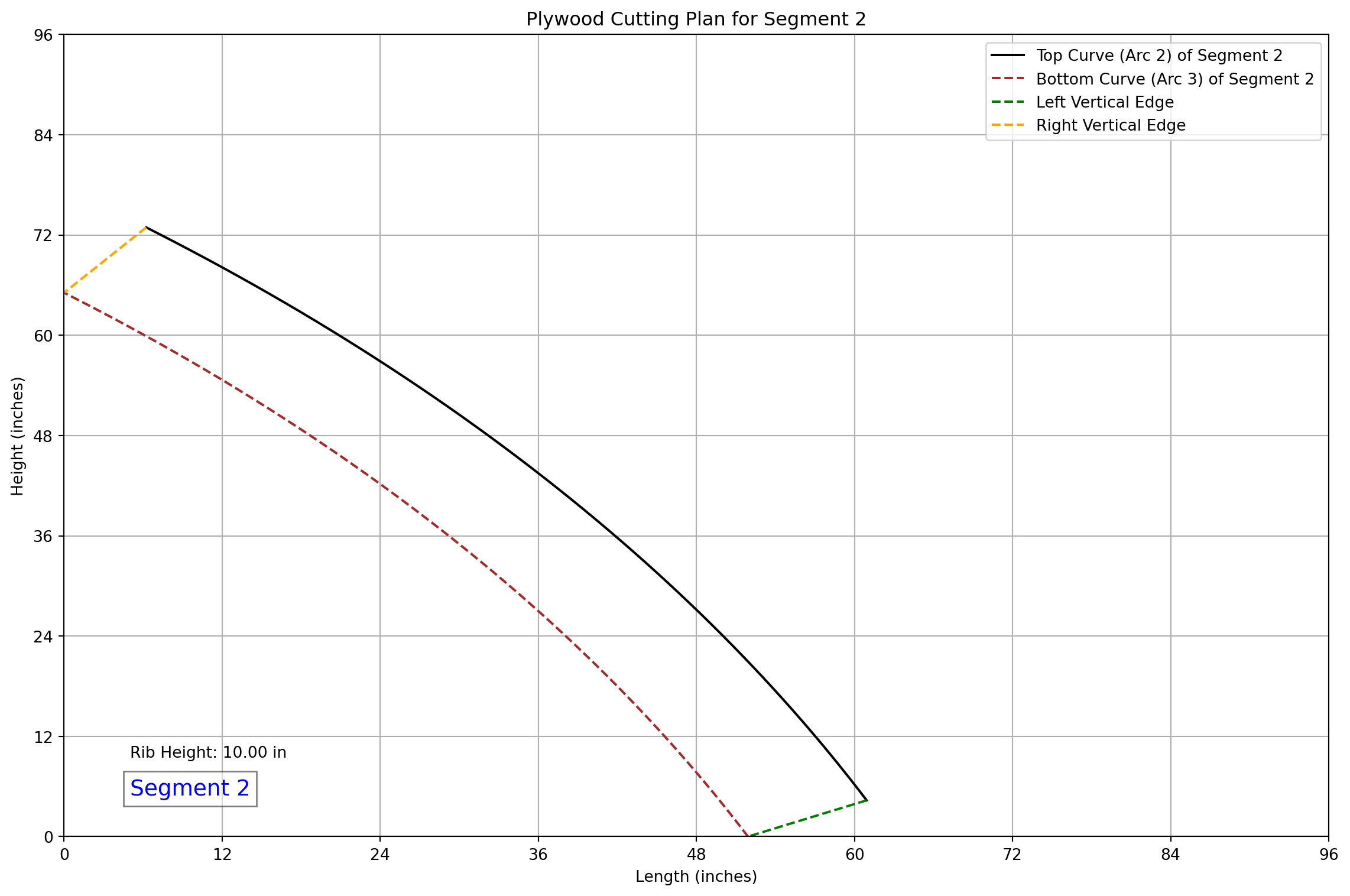
### CNC Cutting Data for Segment 2
- Theta Start: 0.4488 rad, Theta End: 0.8976 rad
- **Top Left**: X: 60.92, Y: 4.34
- **Top Right**: X: 6.23, Y: 72.91
- **Bottom Left**: X: 51.91, Y: 0.00
- **Bottom Right**: X: 0.00, Y: 65.10
- **Arc Length for Segment**: 88.45 inches

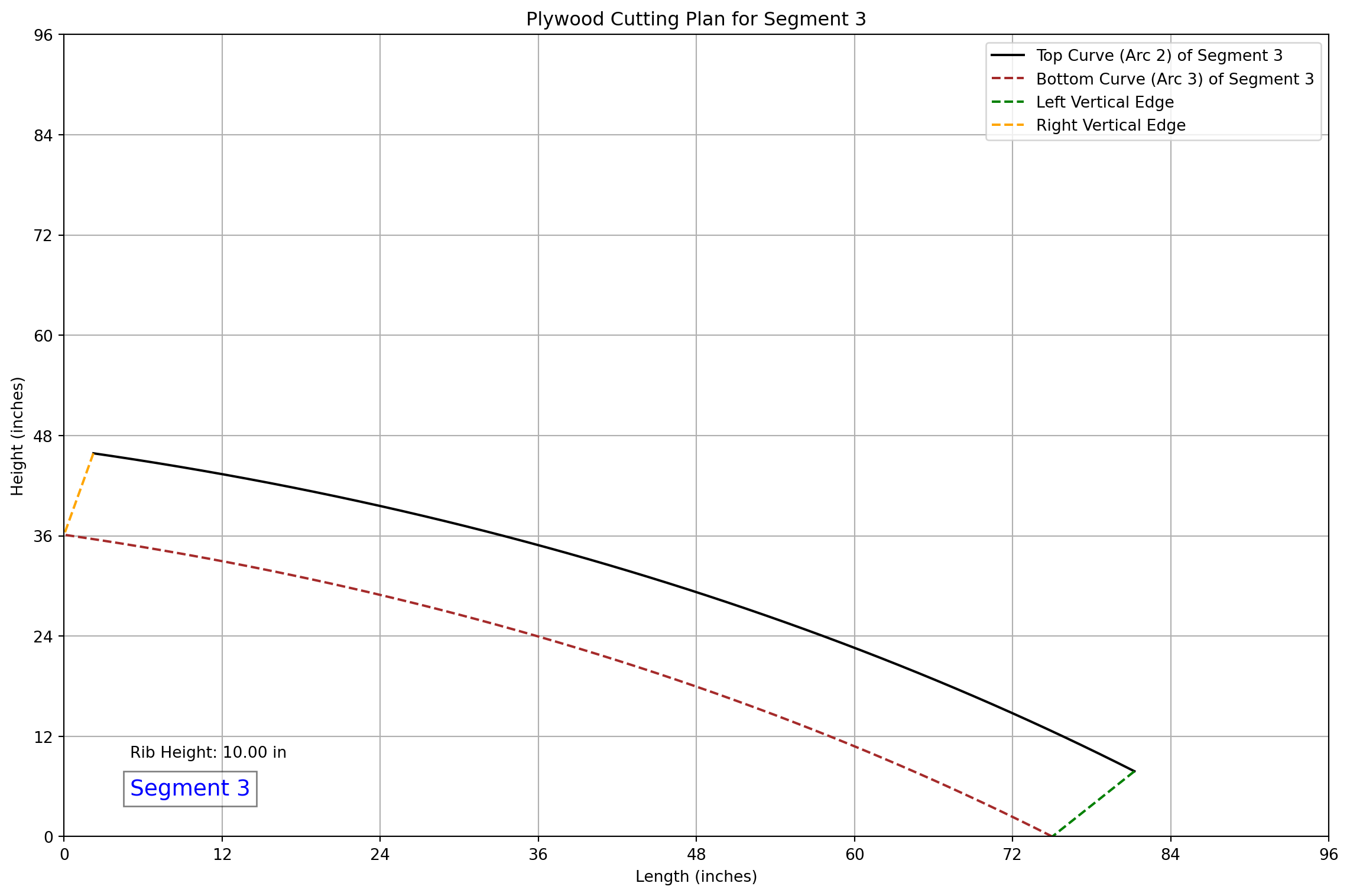
### CNC Cutting Data for Segment 3
- Theta Start: 0.8976 rad, Theta End: 1.3464 rad
- **Top Left**: X: 81.25, Y: 7.82
- **Top Right**: X: 2.23, Y: 45.87
- **Bottom Left**: X: 75.01, Y: 0.00
- **Bottom Right**: X: 0.00, Y: 36.13
- **Arc Length for Segment**: 88.45 inches

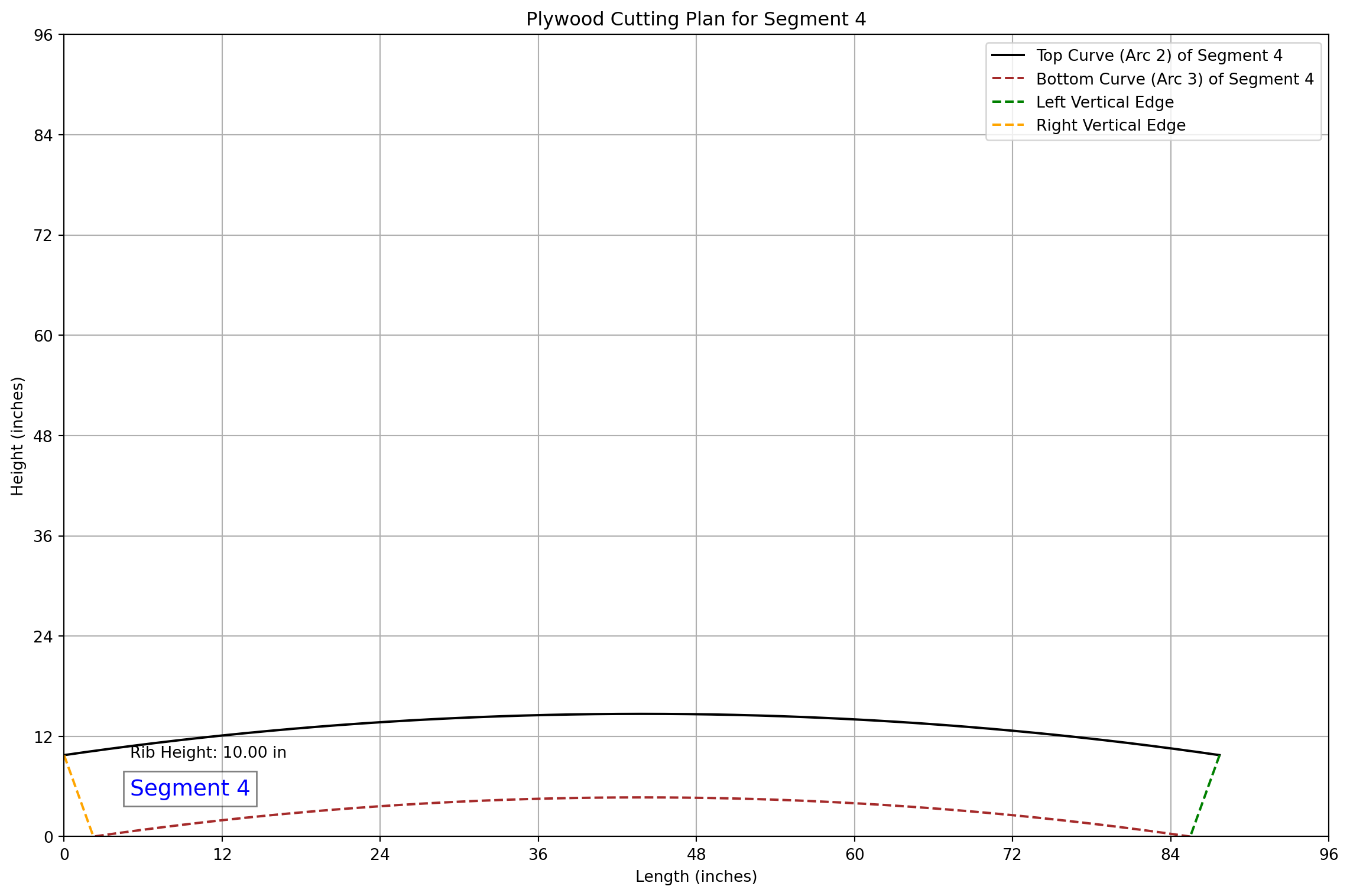
### CNC Cutting Data for Segment 4
- Theta Start: 1.3464 rad, Theta End: 1.7952 rad
- **Top Left**: X: 87.71, Y: 9.75
- **Top Right**: X: 0.00, Y: 9.75
- **Bottom Left**: X: 85.48, Y: 0.00
- **Bottom Right**: X: 2.23, Y: 0.00
- **Arc Length for Segment**: 88.45 inches

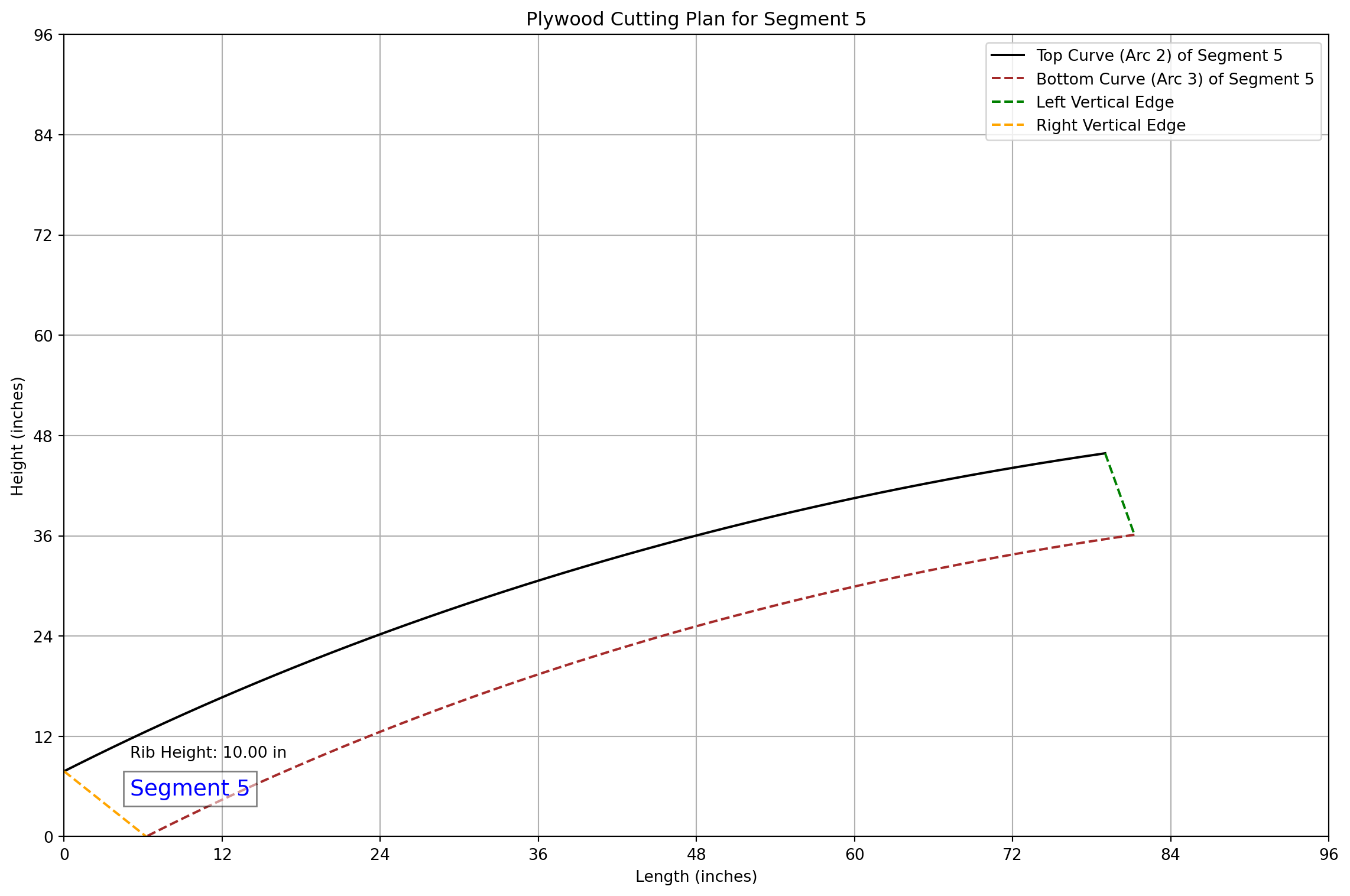
### CNC Cutting Data for Segment 5
- Theta Start: 1.7952 rad, Theta End: 2.2440 rad
- **Top Left**: X: 79.02, Y: 45.87
- **Top Right**: X: 0.00, Y: 7.82
- **Bottom Left**: X: 81.25, Y: 36.13
- **Bottom Right**: X: 6.23, Y: 0.00
- **Arc Length for Segment**: 88.45 inches

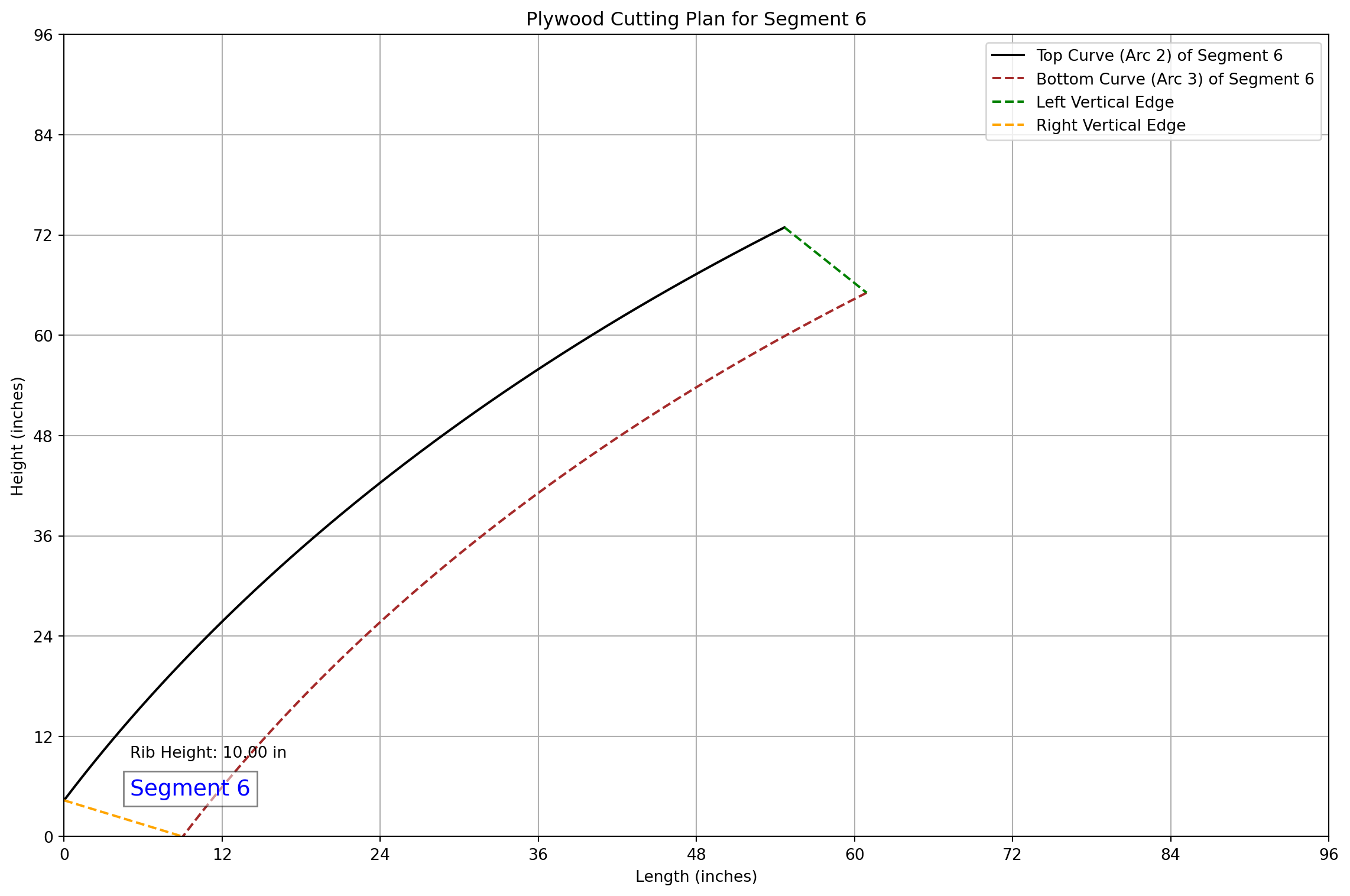
### CNC Cutting Data for Segment 6
- Theta Start: 2.2440 rad, Theta End: 2.6928 rad
- **Top Left**: X: 54.69, Y: 72.91
- **Top Right**: X: 0.00, Y: 4.34
- **Bottom Left**: X: 60.92, Y: 65.10
- **Bottom Right**: X: 9.01, Y: 0.00
- **Arc Length for Segment**: 88.45 inches

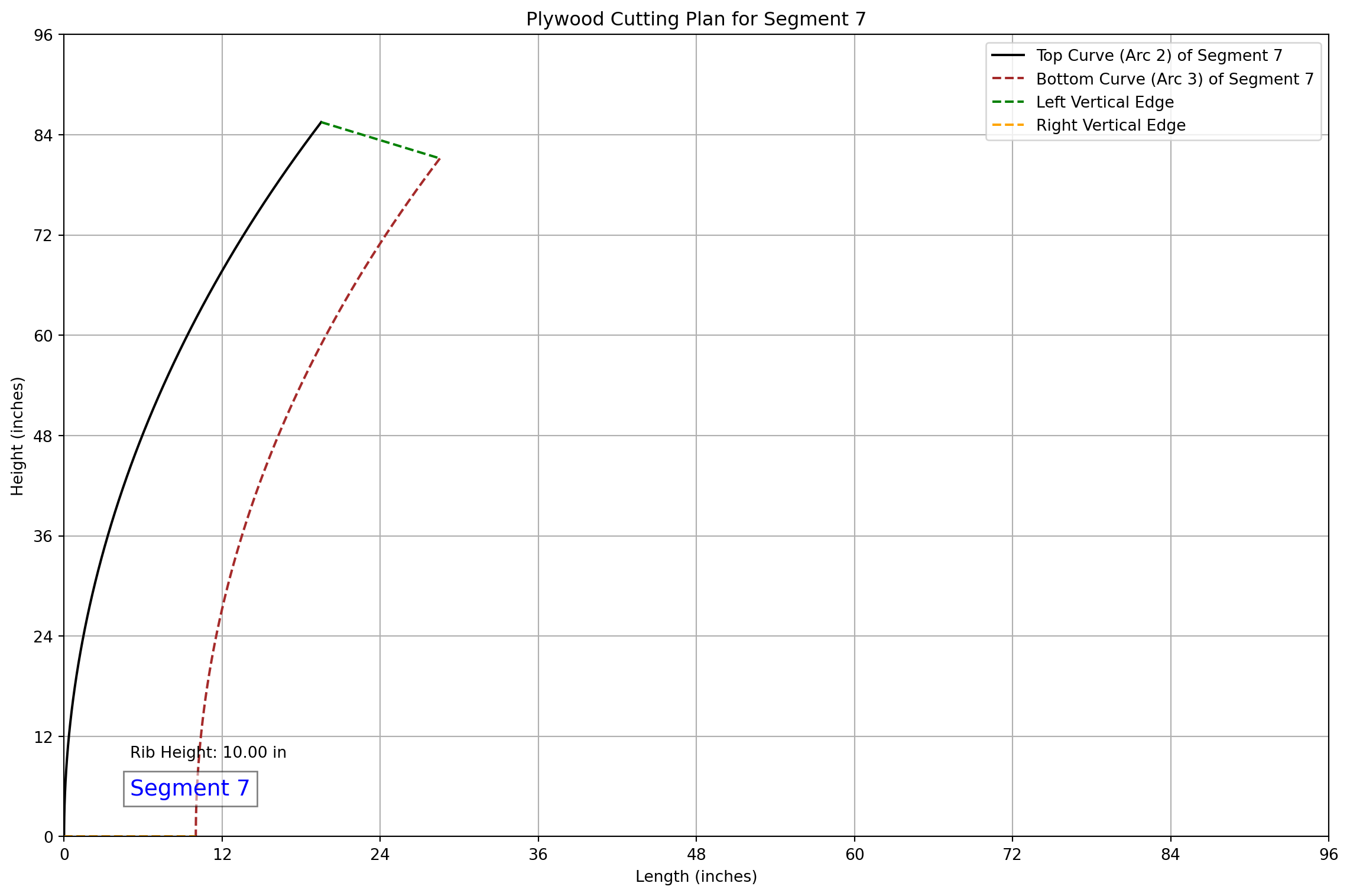
### CNC Cutting Data for Segment 7
- Theta Start: 2.6928 rad, Theta End: 3.1416 rad
- **Top Left**: X: 19.52, Y: 85.51
- **Top Right**: X: 0.00, Y: 0.00
- **Bottom Left**: X: 28.53, Y: 81.17
- **Bottom Right**: X: 10.00, Y: 0.00
- **Arc Length for Segment**: 88.45 inches


## Raw Markdown Data for Fabricators & Installers

Segment 1:
- Theta Start: 0.0000 rad, Theta End: 0.4488 rad
- Top Left: (np.float64(28.52704214853594), np.float64(0.0)), Top Right: (np.float64(9.00968867902418), np.float64(85.51111273459507))
- Bottom Left: (np.float64(18.52704214853594), np.float64(0.0)), Bottom Right: (np.float64(0.0), np.float64(81.17227534341949))
- Arc Length: 88.45 inches

Segment 2:
- Theta Start: 0.4488 rad, Theta End: 0.8976 rad
- Top Left: (np.float64(60.92130720785383), np.float64(4.338837391175588)), Top Right: (np.float64(6.234898018587273), np.float64(72.91342552370905))
- Bottom Left: (np.float64(51.91161852882965), np.float64(0.0)), Bottom Right: (np.float64(0.0), np.float64(65.09511069902875))
- Arc Length: 88.45 inches

Segment 3:
- Theta Start: 0.8976 rad, Theta End: 1.3464 rad
- Top Left: (np.float64(81.24936022385515), np.float64(7.8183148246803)), Top Right: (np.float64(2.2252093395631505), np.float64(45.87434016337187))
- Bottom Left: (np.float64(75.01446220526788), np.float64(0.0)), Bottom Right: (np.float64(0.0), np.float64(36.125061041553636))
- Arc Length: 88.45 inches

Segment 4:
- Theta Start: 1.3464 rad, Theta End: 1.7952 rad
- Top Left: (np.float64(87.71019032907463), np.float64(9.749279121818233)), Top Right: (np.float64(0.0), np.float64(9.749279121818262))
- Bottom Left: (np.float64(85.48498098951148), np.float64(0.0)), Bottom Right: (np.float64(2.2252093395631505), np.float64(2.842170943040401e-14))
- Arc Length: 88.45 inches

Segment 5:
- Theta Start: 1.7952 rad, Theta End: 2.2440 rad
- Top Left: (np.float64(79.02415088429204), np.float64(45.87434016337181)), Top Right: (np.float64(0.0), np.float64(7.8183148246803))
- Bottom Left: (np.float64(81.24936022385519), np.float64(36.12506104155358)), Bottom Right: (np.float64(6.23489801858733), np.float64(0.0))
- Arc Length: 88.45 inches

Segment 6:
- Theta Start: 2.2440 rad, Theta End: 2.6928 rad
- Top Left: (np.float64(54.68640918926657), np.float64(72.91342552370902)), Top Right: (np.float64(0.0), np.float64(4.338837391175588))
- Bottom Left: (np.float64(60.9213072078539), np.float64(65.09511069902872)), Bottom Right: (np.float64(9.00968867902418), np.float64(0.0))
- Arc Length: 88.45 inches

Segment 7:
- Theta Start: 2.6928 rad, Theta End: 3.1416 rad
- Top Left: (np.float64(19.517353469511818), np.float64(85.51111273459516)), Top Right: (np.float64(0.0), np.float64(1.2246467991473515e-15))
- Bottom Left: (np.float64(28.527042148535998), np.float64(81.17227534341957)), Bottom Right: (np.float64(10.0), np.float64(0.0))
- Arc Length: 88.45 inches

---

Conclusion

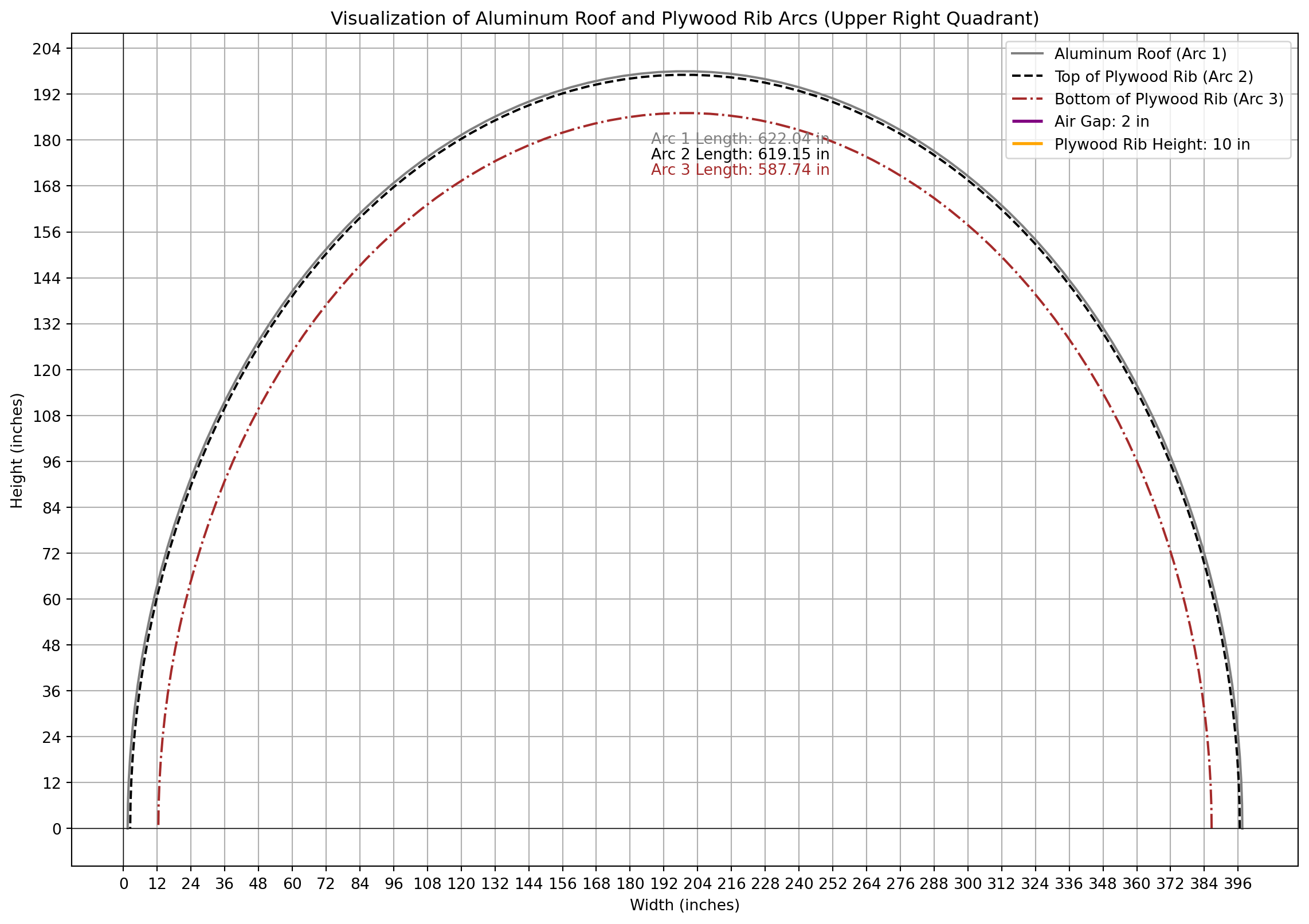
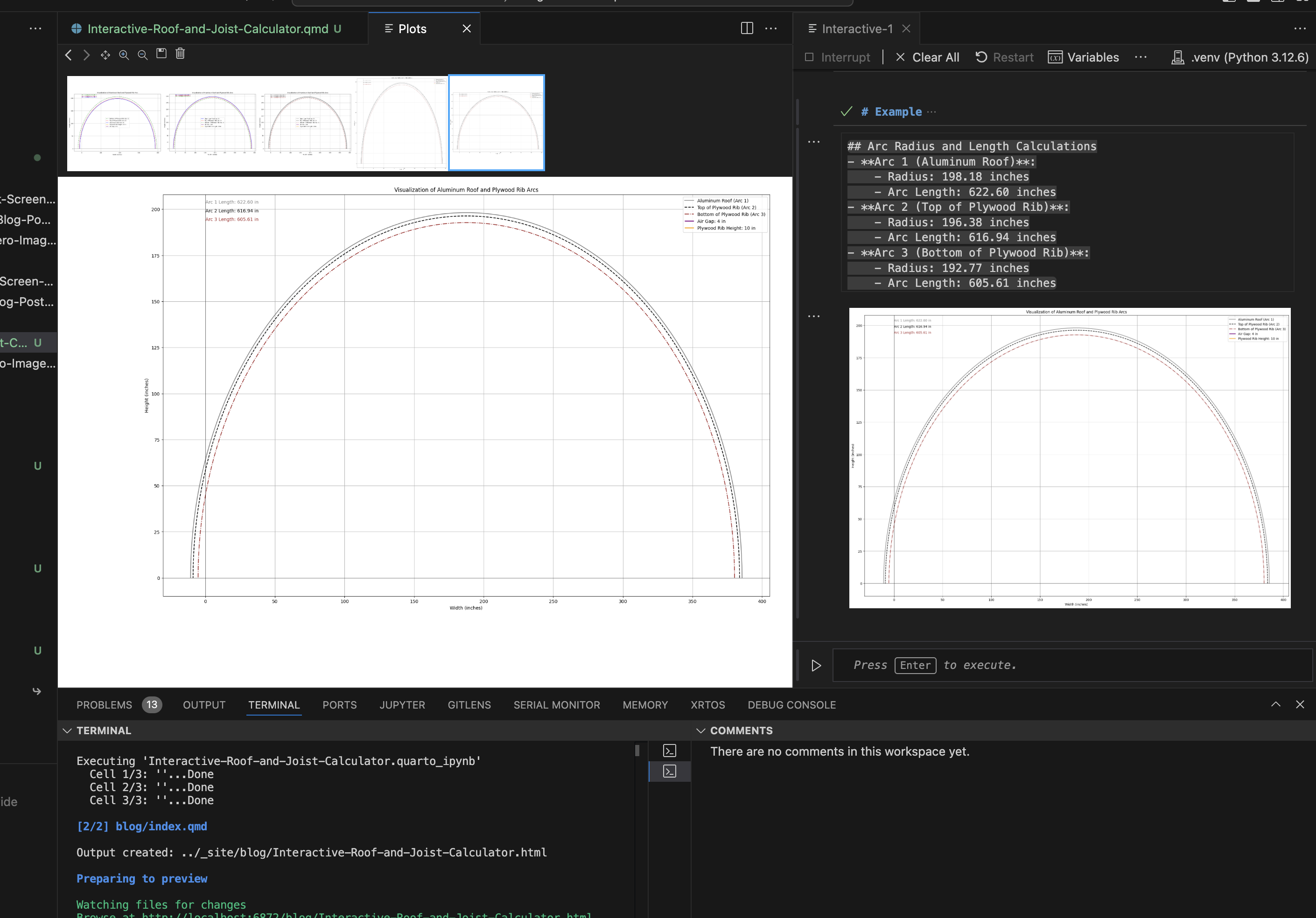This guide provides starting point for calculating and visualizing our aluminum roof arc and the plywood rib-joist arcs. Using Python, we automate the calculation of radii, arc lengths, and segments for CNC cutting. The results are visualized with detailed plots for CNC fabrication and installation.